MAS

Una partícula describe un Movimiento Armónico Simple (M.A.S.) cuando se mueve a lo largo del eje X, estando su posición x dada en función del tiempo t por la ecuación
x=A·sen(ωt+φ)

donde

• A es la amplitud.
• w la frecuencia angular.
• w t+j la fase.
• j la fase inicial.

Las características de un M.A.S. son:

• Como los valores máximo y mínimo de la función seno son +1 y -1, el movimiento se realiza en una región del eje X comprendida entre -A y +A.

• La función seno es periódica y se repite cada 2p, por tanto, el movimiento se repite cuando el argumento de la función seno se incrementa en 2p, es decir, cuando transcurre un tiempo P tal que w(t+P)+j=w t+j+2p .

P=2π/ω

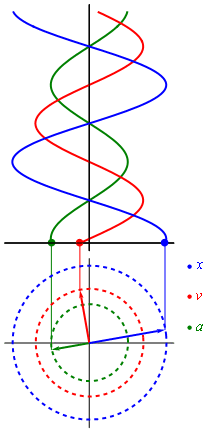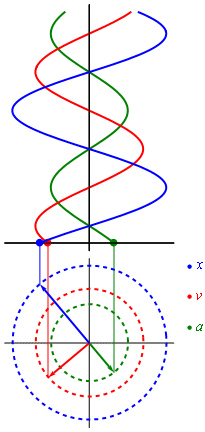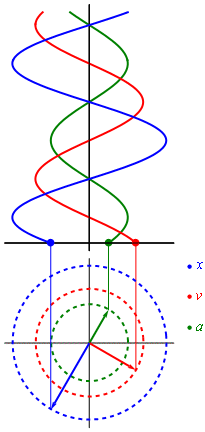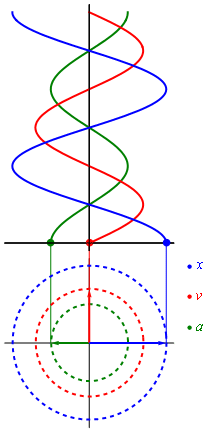
Evolución en el tiempo del desplazamiento, la velocidad y la aceleración en un movimiento armónico simple

Cinemática de un M.A.S.
En un movimiento rectilíneo, dada la posición de un móvil, obtenemos  la velocidad derivando respecto del tiempo y luego, la aceleración derivando la expresión de la velocidad.

La posición del móvil que describe un M.A.S. en función del tiempo viene dada por la ecuación
x=A·sen(ωt+φ)
Derivando con respecto al tiempo, obtenemos la velocidad del móvil

Derivando de nuevo respecto del tiempo, obtenemos la aceleración del móvil

Este resultado se suele expresar en forma de ecuación diferencial

Esta es la ecuación diferencial de un MAS donde x puede ser cualquier magnitud: un desplazamiento lineal, un desplazamiento angular, la carga de un condensador, una temperatura, etc.
Puede comprobarse que la solución de esta ecuación diferencial es
x=A
Condiciones iniciales
Conociendo la posición inicial x₀ y la velocidad inicial v₀ en el instante t=0.
x₀=A·senj
v₀=Aw·cosj
se determinan la amplitud A y la fase inicial φ
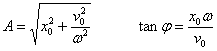sen(w t+j )

 

Dinámica de un M.A.S.

Aplicando la segunda ley de Newton obtenemos la expresión de la fuerza necesaria para que un móvil de masa m describa un M.A.S. Esta fuerza es proporcional al desplazamiento x y de sentido contrario a éste.

Como la  fuerza  F es conservativa. El trabajo de dicha fuerza es igual a la diferencia entre el valor inicial y el final de la energía potencial E_p.

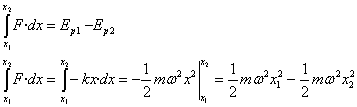
La expresión de la energía potencial es

Donde c es cualquier constante. Se toma como nivel cero de la energía potencial E_p=0 cuando el móvil está en el origen, x=0, por lo que c=0
La energía total E, es la suma de la energía cinética E_k y de la energía potencial E_p que es constante.




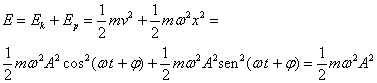
Péndulo

El péndulo (del lat. pendŭlus, pendiente)^[1] es un sistema físico que puede oscilar bajo la acción gravitatoria u otra característica física (elasticidad, por ejemplo) y que está configurado por una masa suspendida de un punto o de un eje horizontal fijos mediante un hilo, una varilla, u otro dispositivo.

Existen muy variados tipos de péndulos que, atendiendo a su configuración y usos, reciben los nombres apropiados: péndulo simple, péndulo compuesto, péndulo cicloidal, doble péndulo, péndulo de Foucault, péndulo de Newton, péndulo balístico, péndulo de torsión, péndulo esférico, etcétera.

Sus usos son muy variados: medida del tiempo (reloj de péndulo, metrónomo, ...), medida de la intensidad de la gravedad, etc.

Energía en el M.A.S.

graficos

Osciladores amortiguados

Introducción

La experiencia nos muestra que la amplitud de un cuerpo vibrante tal como un resorte o un péndulo, decrece gradualmente hasta que se detiene.

Para explicar el amortiguamiento, podemos suponer que además de la fuerza elástica F = -kx, actúa otra fuerza opuesta a la velocidad F' = -ðv, donde ð es una constante que depende del sistema físico particular. Todo cuerpo que se mueve en el seno de un fluido viscoso en régimen laminar experimenta una fuerza de rozamiento proporcional a la velocidad y de sentido contrario a ésta.