Choques o colisiones

El choque se define como la colisión entre dos o más cuerpos, pero también puede definirse como una excitación física.

Un choque físico o mecánico es percibido por una repentina aceleración o desaceleración causada normalmente por un impacto, por ejemplo, de una gota de agua, aunque también una explosión causa choque; cualquier tipo de contacto directo entre dos cuerpos provoca un choque. Lo que mayormente lo caracteriza es la duración del contacto que, generalmente, es muy corta y es entonces cuando se transmite la mayor cantidad de energía entre los cuerpos.

Efectos de choque

La mecánica de choque tiene el potencial de dañar, deformar, etc:

Un cuerpo frágil se puede fracturar. Por ejemplo, dos copas de cristal pueden romperse en caso de colisión una contra el otra. Una cizalla en un motor está diseñada para la fractura con cierta magnitud de choque.
Un objeto ductil se puede doblar por una conmoción (deformar). Por ejemplo, una jarra de cobre se puede curvar cuando cae en el suelo.
Algunos objetos no se dañan por un único choque, pero si se produce fatiga en el material con numerosas repeticiones de choques de bajo nivel.
Un efecto de choque puede resultar sólo daños menores, que pueden no ser críticos para su uso. Sin embargo, daños menores acumulados de varios efectos de choques, eventualmente resultarán en que el objeto sea inutilizable.
Un choque puede no producir daño aparente de inmediato, pero podría reducir la vida útil del producto: la fiabilidad se reduce.
Algunos materiales como los explosivos se pueden detonar con mecánicas de choque o impacto.

Choque elástico

En física, se denomina choque elástico a una colisión entre dos o más cuerpos en la que éstos no sufren deformaciones permanentes durante el impacto. En una colisión elástica se conservan tanto el momento lineal como la energía cinética del sistema, y no hay intercambio de masa entre los cuerpos, que se separan después del choque.

Las colisiones en las que la energía no se conserva producen deformaciones permanentes de los cuerpos y se denominan inelásticas.

Choque elástico de dos partículas

En la página titulada “choques frontales” estudiamos como caso particular, el choque elástico entre dos partículas. En este caso, la primera partícula lleva una velocidad u₁ y la segunda está inicialmente en reposo u₂=0.

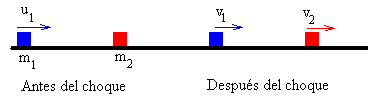
1 Principio de conservación del momento lineal

m₁u₁ =m₁v₁+m₂v₂

2 En un choque elástico, la energía cinética inicial es igual a la final.

Resolviendo este sistema de dos ecuaciones con dos incógnitas, obtenemos las velocidades v₁ y v₂ después del choque

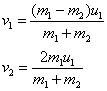
se cumple:

Choque inelástico

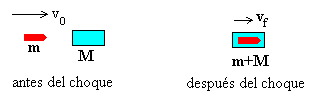
Si M es la masa del bloque inicialmente en reposo, m la masa de la bala. Aplicamos el principio de conservación del momento lineal, a este sistema aislado, para obtener la velocidad inmediatamente después del choque v_f del conjunto bala-bloque en función de la velocidad v₀ de la bala antes del choque.

mv₀=(m+M)v_f

A continuación, se efectúa el balance energético de la colisión. La variación de energía cinética es

Choque inelástico de duración finita

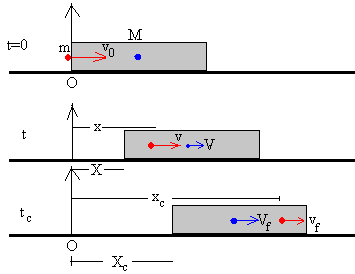
Mediante un modelo simple de interacción entre la bala y el bloque, vamos a explicar cómo la bala disminuye de velocidad, aumenta la del bloque hasta que ambas se igualan. También, explicaremos el origen de la diferencia de energía cinética.

A medida que la bala penetra en el bloque, la bala ejerce una fuerza F que supondremos constante sobre el bloque y su efecto será el de incrementar su velocidad.

A su vez, el bloque ejercerá una fuerza F igual y opuesta sobre la bala cuyo efecto será el de disminuir su velocidad. El choque se completará cuando la velocidad de la bala se iguale a la del bloque.

Tenemos que estudiar la dinámica de un sistema aislado formado por dos partículas que interaccionan entre sí. La interacción se describe en términos de una fuerza constante F.

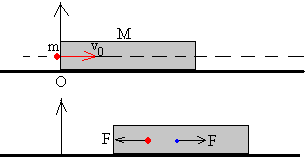
Velocidades antes y después del choque

Cuando la bala penetra, la fuerza constante F que ejerce el bloque hace que disminuya su velocidad.

v=v₀-F·t/m

La fuerza F igual y de sentido contrario que ejerce la bala sobre el bloque hace que éste incremente su velocidad

V= F·t/M

Dado que el sistema formado por la bala y el bloque es aislado, el momento lineal total o la velocidad de su centro de masas v_cm permanece constante e igual a su velocidad inicial como podemos comprobar.

El choque finaliza cuando la velocidad v de la bala se iguala a la velocidad V del bloque, es decir en el instante t_c, medido desde el momento en el que la bala penetra en el bloque.

v₀-F·t_c/m= F·t_c/M

Se cumple: