CANTIDAD DE MOVIMIENTO
La cantidad de movimiento o momento lineal se refiere a objetos en movimientos y es una magnitud vectorial que desempeña un papel muy importante en la segunda ley de Newton. La cantidad de movimiento combina las ideas de inercia y movimiento. También obedece a un principio de conservación que se ha utilizado para descubrir muchos hechos relacionados con las partículas básicas del Universo. La ley de la conservación de la cantidad de movimiento y la ley de la conservación de la energía, son las herramientas más poderosas de la mecánica. La conservación de la cantidad de movimiento es la base sobre la que se construye la solución a diversos problemas que implican dos o más cuerpos que interactúan, especialmente en la comprensión del comportamiento del choque o colisión de objetos.
Fuerzas externas e internas
Al analizar el comportamiento de un sistema de varios cuerpos, es conveniente distinguir entre fuerzas internas y externas. Las fuerzas internas son aquellas por las cuales todas las partes del sistema actúan entre sí. Las fuerzas externas son aquellas que influyen fuera del sistema sobre uno o más de los cuerpos de éste o sobre el sistema completo.
Una experiencia común indica que todo objeto en movimiento posee una cualidad que lo hace ejercer una fuerza sobre todo cuando se le intenta detener. Cuanta mayor sea la rapidez con que se desplaza, más difícil será detenerlo. Además, cuanta mayor masa tenga, más difícil será pararlo. 
Newton le dio el nombre de movimiento a esta cualidad de un objeto en movimiento. Hoy se le llama cantidad de movimiento o momento lineal.
Y se define del modo siguiente.
Cantidad de movimiento = masa x velocidad.
Donde P es el símbolo con que se representa la cantidad de movimiento.
P es un vector que apunta en la misma dirección que V.
Unidades: En el MKS: Kg.m/seg.
CGS: gr.cm/seg.
También puede verse que un barco de grandes dimensiones que navegue a baja velocidad tiene una gran cantidad de movimiento, como lo tiene una bala pequeña disparada a alta velocidad. Y por supuesto, un objeto enorme que se desplace a alta velocidad.
Cuando una bala o un camión chocan contra una pared, se ejerce contra ésta una gran fuerza. ¿De donde proviene tal fuerza? De un cambio de velocidad. La fuerza de impacto es proporcional a la razón de cambio de velocidad del objeto en movimiento. Y a mayor masa de ese objeto, mayor fuerza; así, la fuerza de impacto es también proporcional a la masa del objeto en movimiento.
Variación en la cantidad de movimiento
Cuando ocurre un cambio en la masa y en la velocidad, en ambas a la vez, existirá un cambio en la cantidad de movimiento del cuerpo considerado.
Si la masa permanece constante pero la velocidad del cuerpo cambia de V1 a V2 se tendrá que:
La variación de la cantidad e movimiento será:
Estas ideas son congruentes con la segunda ley de Newton,
La segunda ley de newton, en terminos de la cantidad de movimiento,establece que la fuerza sobre un objeto es igual a la rapidez de cambio de la cantidad de movimiento del objeto,es decir:
Una bala se acelera cuando se ejerce una fuerza sobre ella. Cuán rápido se mueva al final, no obstante, depende de algo además de su masa y la fuerza impartida. La velocidad final depende del tiempo. Una fuerza sostenida por un tiempo largo empuja la bala a una velocidad mayor que la misma fuerza aplicada brevemente.
Se puede expresar la segunda ley de Newton de otra forma, haciendo más evidente el factor tiempo, sustituyendo el término para la aceleración por su definición (v/t).
Cantidad de movimiento de un sistema de partículas La cantidad total de movimiento del sistema de partículas es la suma vectorial de las cantidades vectoriales de las partículas individuales. Es decir: 
= 
+ 
+ 
+ ... 
ejemplo de tres partículas:
Sumatoria de las componentes según el eje x :
Px = P1x + P2x + P3xSumatoria de las componentes según el eje y:
Py = P1y + P2y + P3y
Los componentes Px y Pyse representa en un sistema ejes rectangulares y se determina el vector cantidad de movimiento cuyo módulo es: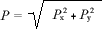 
El anterior procedimiento es válido para un número cualquiera de partículas.
IMPULSO
En mecánica, se llama impulso a la magnitud física, denotada usualmente como I, definida como la variación en el momento lineal que experimenta un objeto en un sistema cerrado. El término difiere de lo que cotidianamente conocemos como impulso y fue acuñado por Isaac Newton en su segunda ley, donde lo llamó vis motrix, refiriéndose a una especie de fuerza del movimiento.
Si consideramos una masa que no varía en el tiempo sujeta a la acción de una fuerza también constante, la cantidad de movimiento se puede tomar como el simple producto entre la velocidad y la masa . Según la segunda ley de Newton, si a una masa m se le aplica una fuerza 
aquélla adquiere una aceleración a, de acuerdo con la expresión:
aquélla adquiere una aceleración a, de acuerdo con la expresión:
F = m a
multiplicando ambos miembros por el tiempo en que se aplica la fuerza:
FxT= m a (T)
y finalmente:
I = FxT
Relaciones entre el impulso y la cantidad de movimiento.
La segunda ley de Newton expresa que F= m.a; Como a = v/t se puede escribir: F= m.(v/t); Luego F.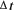 
= m.
para concluir que I= F. , es decir el cambio de la cantidad de movimiento es el producto de la fuerza F (su promedio respecto al tiempo) y el intervalo de tiempo a lo largo del cual actúa dicha fuerza).
= m.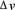 para concluir que I= F. 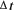, es decir el cambio de la cantidad de movimiento es el producto de la fuerza F (su promedio respecto al tiempo) y el intervalo de tiempo 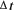a lo largo del cual actúa dicha fuerza).
El producto F. 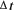; Se denomina impulso.
; Se denomina impulso. 
Teorema del impulso y de cantidad de movimientoEl impulso resultante ejercido sobre una partícula durante cierto intervalo de tiempo es igual a la variación de la cantidad de movimiento de la partícula.
El impulso, para el cual no se utiliza ningún signo convencional, es una cantidad vectorial dirigida a lo largo de la fuerza media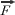 
. Tiene las mismas unidades y dimensiones que la cantidad de movimiento, aunque se acostumbra, al tratar sobre impulso, usar la unidad Newton segundo (MKS) y Dina segundo (CGS).
. Tiene las mismas unidades y dimensiones que la cantidad de movimiento, aunque se acostumbra, al tratar sobre impulso, usar la unidad Newton segundo (MKS) y Dina segundo (CGS). Centro de masa de un sistema de partículas(C.M)
Sea un sistema de partículas de "n" partículas:
¿Cómo se vincula el centro de masa con el sistema de partículas?
No hay comentarios:
Publicar un comentario